树
数据结构、算法

1. 概念
说到树,就得先说下线性结构和非线性结构。数据结构存在的意义就是去构造一组相互关联的数据模型,然后再配合算法,一起解决计算机中一些运行一些需要耗时的操作。线性和非线形就是非常重要的两种数据模型。
- 线性结构: 数据元素关系是一对一的,数据元素是首尾呼应
- 栈
- 队列
- 线性表
- 数组
- 串
- 非线形结构: 元素之间关系不是一对一,每个元素可能与零个或多个其他数据有关系
- 二维数组
- 多维数组
- 广义表
- 树
- 图
所以树的概念就非常明了了,是一种非线形结构,有一个根,根下的每一层都是子节点,也是构成一棵树,典型的递归。这种数据逻辑结构其实使用的非常广,比如在数据库系统中数据信息的组织形式,操作系统中文件系统的分层管理等等,还有我们写代码,一层一层的也是这种结构,使用这种结构也是非常明显的一个好处,便于搜索查找。

2. 二叉树
二叉树是一种比较简单的树形结构,就是每个节点最多有两个子树,最少是0个。
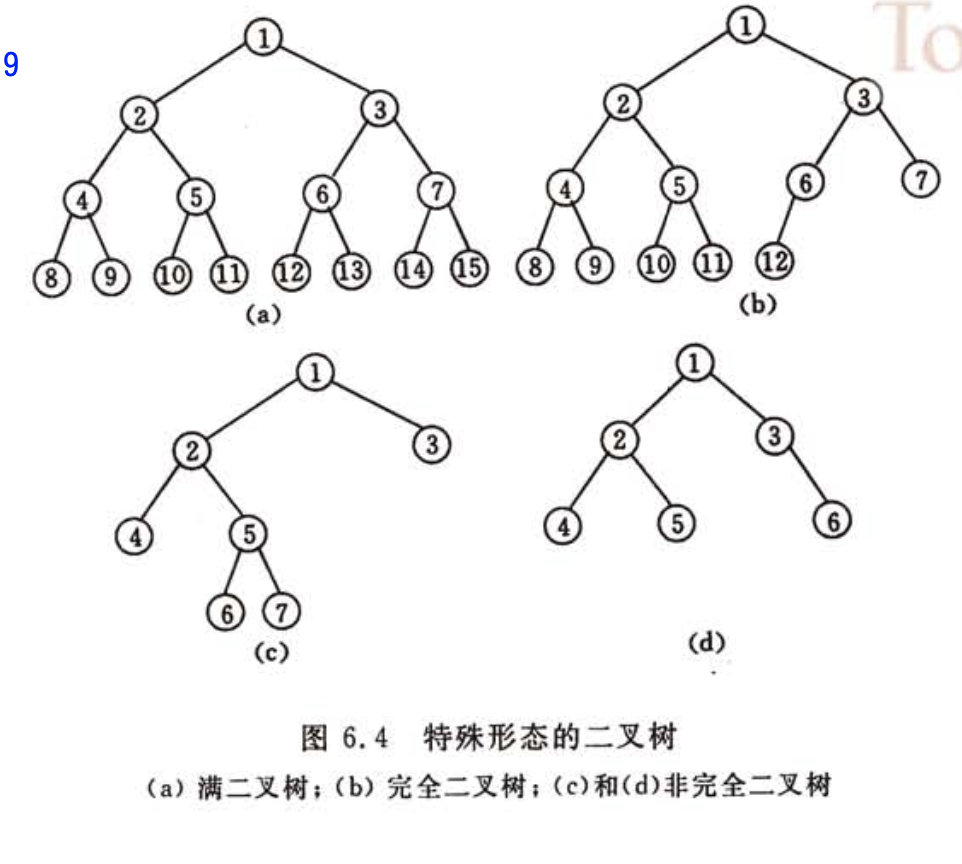
3. 二叉树的遍历
3.1 构造二叉树
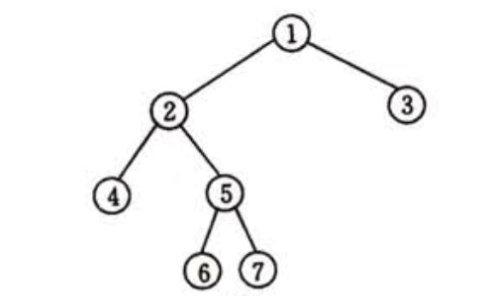
代码演示。
3.2 二叉树遍历
-
前序遍历
-
中序遍历
-
后续遍历
代码演示
3.4 求二叉树的最大值
代码演示
3.5 求二叉树的最大深度
代码演示
4. 二叉搜索树(BST)
4.1 概念
也叫二叉查找树,BST, Binary Search Tree, 它的要求是: 左子树下的节点值小于节点值,右子树下的每个节点值大于节点值。
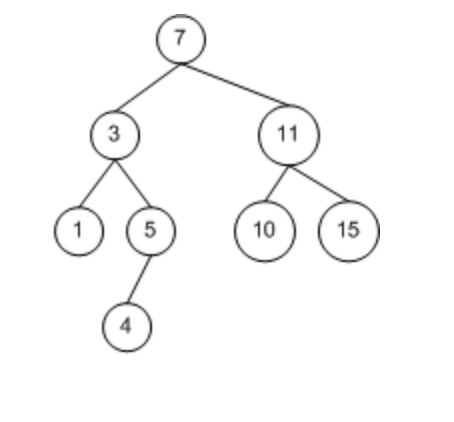
为啥要搞出这玩意,其实很明显,能够提高查找的效率,其实它就是一个二分查找。它的时间复杂度是依赖于二叉树的拓扑结构,也就是和它的深度有关。最差的情况就是O(n), 最好的时候就是 O (log2 (n)).
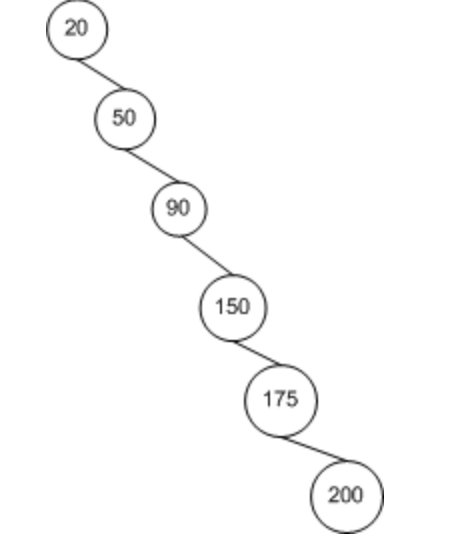
4.2 构造二叉搜索树
比如给一组数组,arr[] = {6, 4, 5, 9, 2, 3, 7, 8, 1}, 构造一棵二叉搜索树。
代码演示。
构造二叉树的中序遍历是数组的排序。
4.3 平衡二叉树
刚刚讲了二叉搜索树的时间复杂度是和它的深度有关,深度越深,时间复杂度越高,平衡二叉树来了。
概念: 平衡二叉树(Balanced Binary Tree), 也叫AVL树。 首先,平衡二叉树肯定是一棵二叉搜索树,其次,它的左右两个子树的高度差的绝对值不超过1,而且左右两个子树都是一棵平衡二叉树。
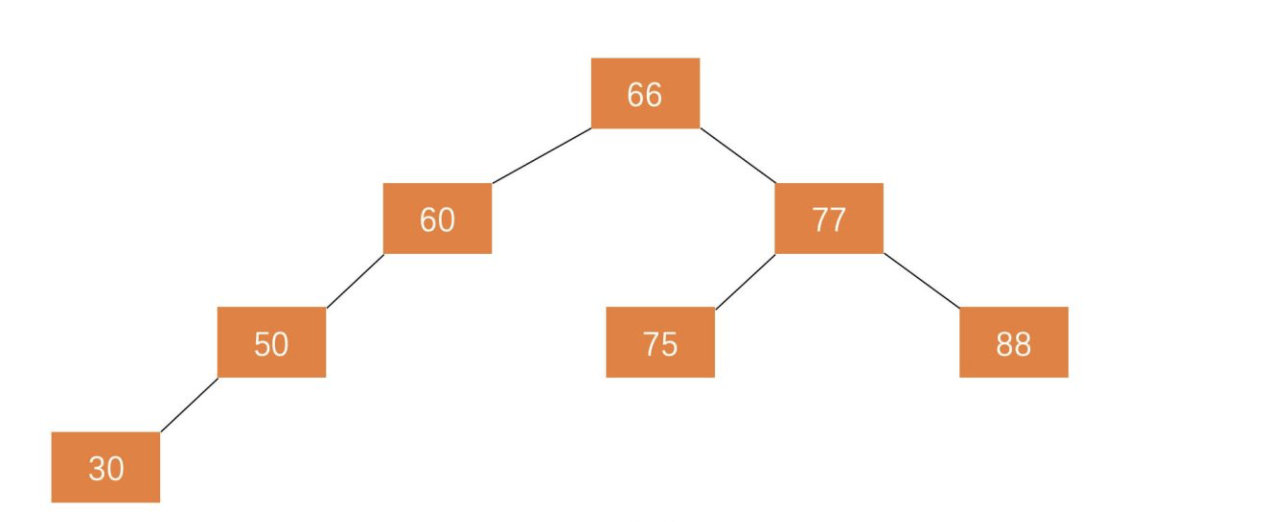
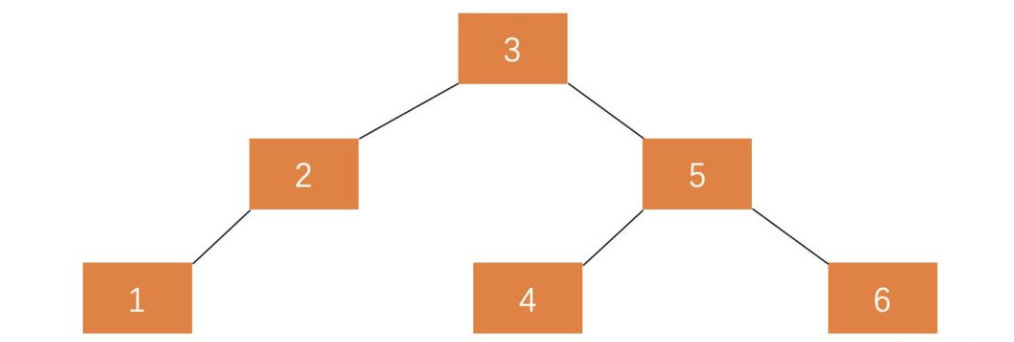
二叉搜索树可以通过平衡因子对搜索树进行调整。
5. 深度优先搜索和广度优先搜索
这两种方式都是对树形结构进行遍历的两种方式,一种是深度遍历,一种是依树的层次进行遍历。
5.1 深度优先搜索 (DFS)
深度优先搜索,就是Depth-First-Search, 缩写的DFS算法。二叉树的前序中序后序遍历就是DFS算法。我就不举例子了。
5.2 广度优先搜索 (BFS)
广度优先搜索,就是Breadth-First-Search, 缩写为BFS算法。就是依树的层次进行遍历。
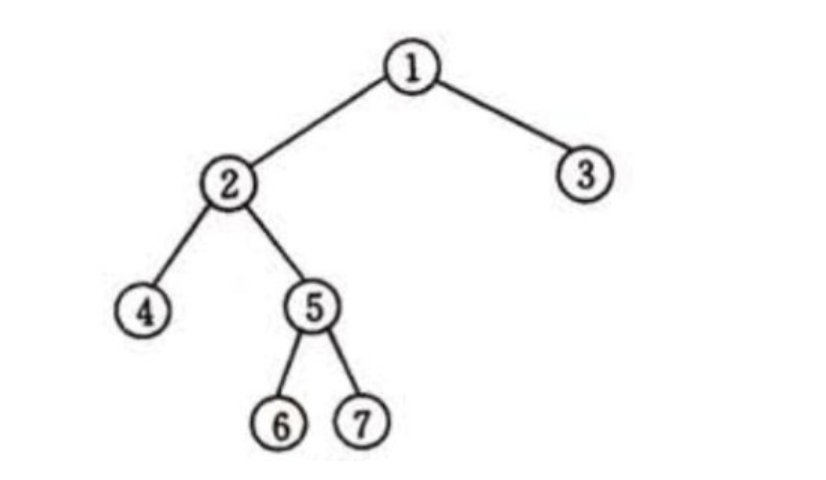
比如这棵树,广度优先搜索,[1, 2, 3, 4, 5, 6, 7]; 代码实现是通过队列来实现。