tree

1. Concept

When it comes to trees, we must first talk about linear structures and nonlinear structures. The meaning of the data structure is to construct a set of interrelated data models, and then cooperate with the algorithm to solve some time-consuming operations in the computer. Linear and nonlinear are two very important data models.

• Linear structure: The relationship between data elements is one-to-one, and the data elements echo each other
  • stack
  • queue
  • linear table
  • array
  • string
• Non-linear structure: the relationship between elements is not one-to-one, and each element may have a relationship with zero or more other data
  • Two-dimensional array
  • Multidimensional Arrays
  • generalized table
  • Tree
  • picture

So the concept of a tree is very clear. It is a nonlinear structure with a root, and each layer under the root is a child node, which also constitutes a tree, a typical recursion. This kind of data logic structure is actually widely used, such as the organizational form of data information in the database system, the hierarchical management of the file system in the operating system, etc., and when we write code, the layer-by-layer structure is also the same. Using this structure is also a very obvious benefit, which is easy to search and find.

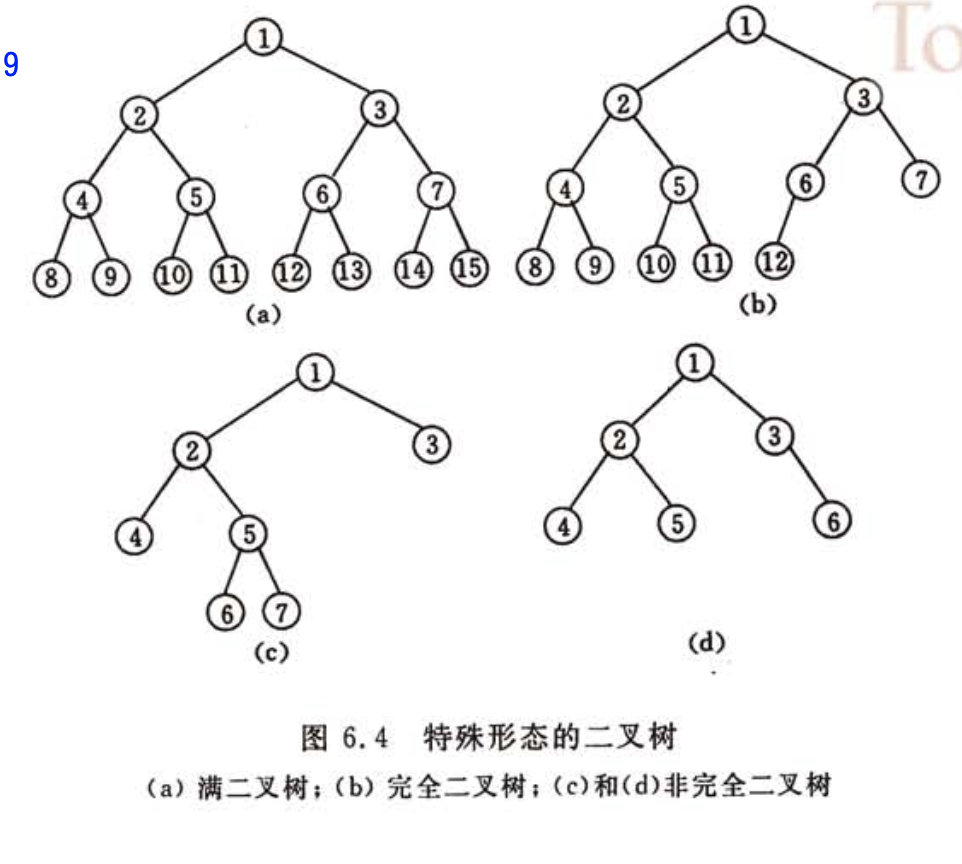
2. Binary tree

A binary tree is a relatively simple tree structure, that is, each node has at most two subtrees, and at least 0.

3. Binary tree traversal

3.1 Construct a binary tree

Code demo.

3.2 Binary tree traversal

• Preorder traversal

• Inorder traversal

• Subsequent traversal

  code demo

3.4 Find the maximum value of the binary tree

Code Demo

3.5 Find the maximum depth of the binary tree

Code Demo

4. Binary Search Tree (BST)

4.1 Concept

Also called binary search tree, BST, Binary Search Tree, its requirement is: the node value under the left subtree is smaller than the node value, and the value of each node under the right subtree is greater than the node value.

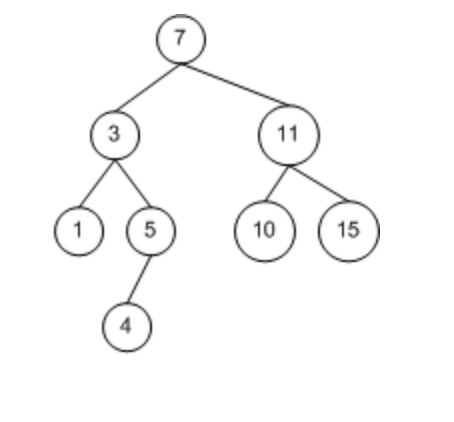
Why do you want to come up with this thing? In fact, it is obvious that it can improve the efficiency of search. In fact, it is a binary search. Its time complexity depends on the topology of the binary tree, which is related to its depth. Worst case is O(n), best case is O(log2 (n)).

4.2 Construct a binary search tree

For example, given a set of arrays, arr[] = {6, 4, 5, 9, 2, 3, 7, 8, 1}, construct a binary search tree.

Code demo.

The inorder traversal for constructing a binary tree is the sorting of the array.

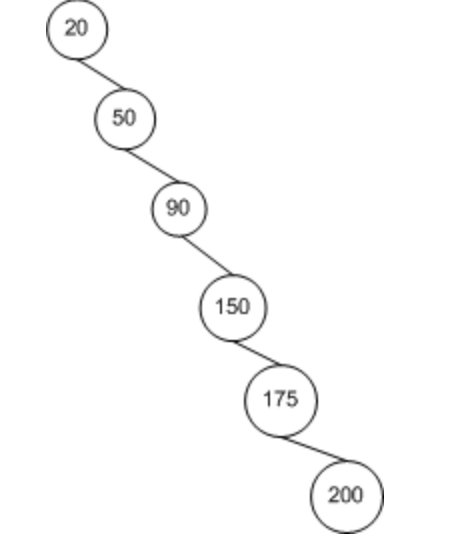
4.3 Balanced binary tree

I just said that the time complexity of a binary search tree is related to its depth. The deeper the depth, the higher the time complexity. Here comes the balanced binary tree.

Concept: Balanced Binary Tree (Balanced Binary Tree), also called AVL tree. First, a balanced binary tree must be a binary search tree. Secondly, the absolute value of the height difference between its left and right subtrees does not exceed 1, and both left and right subtrees are a balanced binary tree.

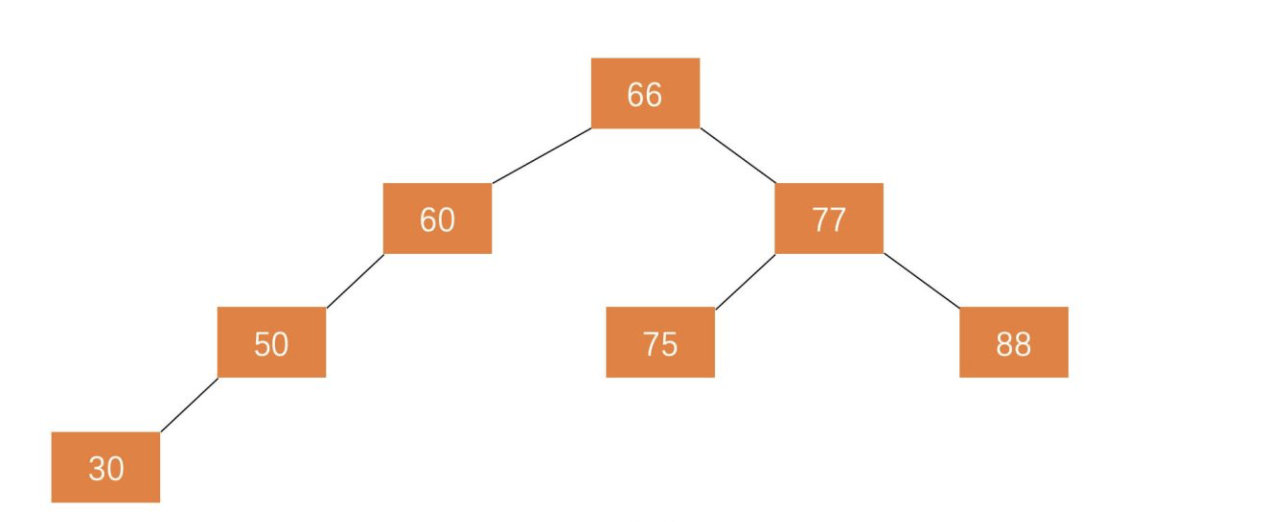
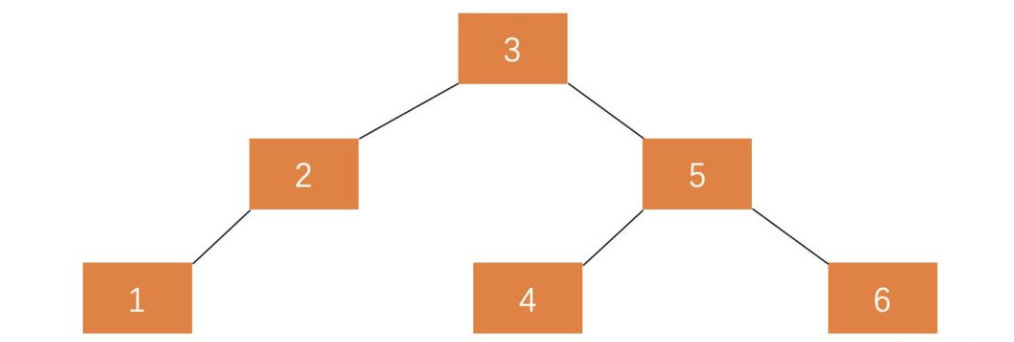
The binary search tree can adjust the search tree through the balance factor.

5. Depth-first search and breadth-first search

These two methods are two ways to traverse the tree structure, one is deep traversal, and the other is traversal by tree level.

5.1 Depth-First Search (DFS)

Depth-first search is Depth-First-Search, the abbreviated DFS algorithm. The pre-order, in-order and post-order traversal of a binary tree is the DFS algorithm. I will not give an example.

5.2 Breadth First Search (BFS)

Breadth-First Search is Breadth-First-Search, abbreviated as BFS algorithm. It is to traverse according to the level of the tree.

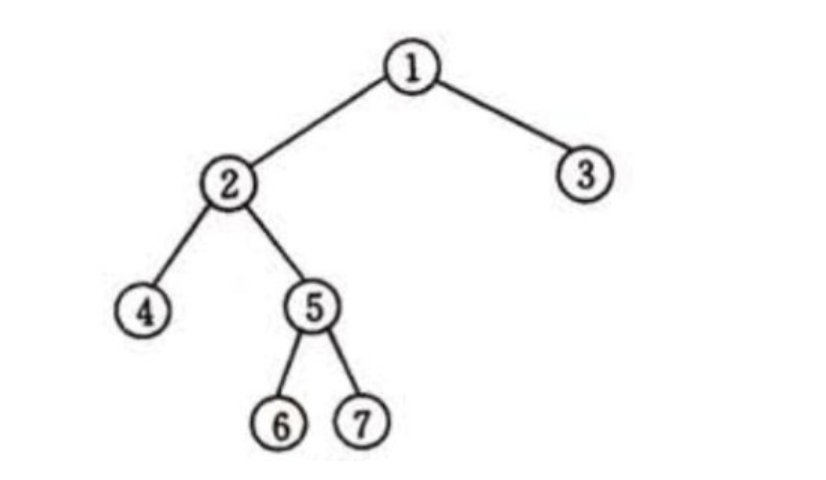
For example, this tree, breadth-first search, [1, 2, 3, 4, 5, 6, 7]; the code implementation is realized through the queue.

5.3 DFS and BFS specific example scenarios